ビジネスや科学的な分野でよく目にする箱ひげ図は、Excel(エクセル)を使用して作成することができます。ばらつきのあるデータの特徴を可視化する時に使用されますが、扱い方をしらないと作成が難しいかもしれません。
この記事ではグラフの作成だけでなく、箱ひげ図の見方や外れ値の確認方法まで丁寧に解説していますのでぜひ参考にしてください。
Excelの箱ひげ図とは
Excel(エクセル)の箱ひげ図とは、アメリカの数学者・統計学者であるジョン・テューキーが考え出したものです。「箱」と「ひげ」のような図形の組み合わせ、1つの図形でデータの分布を把握することができます。
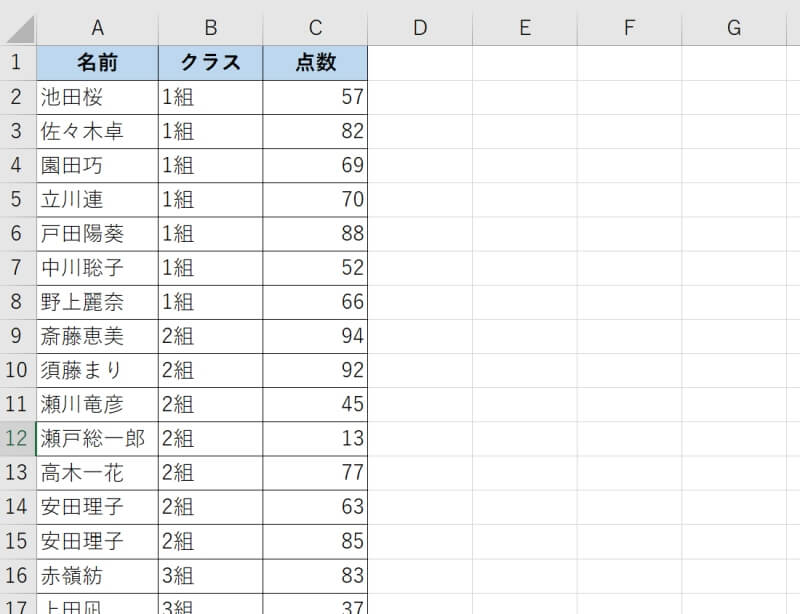
散布図やヒストグラムよりは直感的には分かりづらいかもしれませんが、慣れれば非常に多くの情報をまとめることができるので使い方を練習してみましょう。
箱ひげ図ではデータの最大値、最小値、中央値、第1四分位数、第3四分位数が一目で分かります。それぞれの統計用語の詳細は後述する表を参考にしてください。
このような分布の特徴が1つの図形で表されるので、この図形を並べて複数のデータの分布の様子を一括で比較するために用いられます。
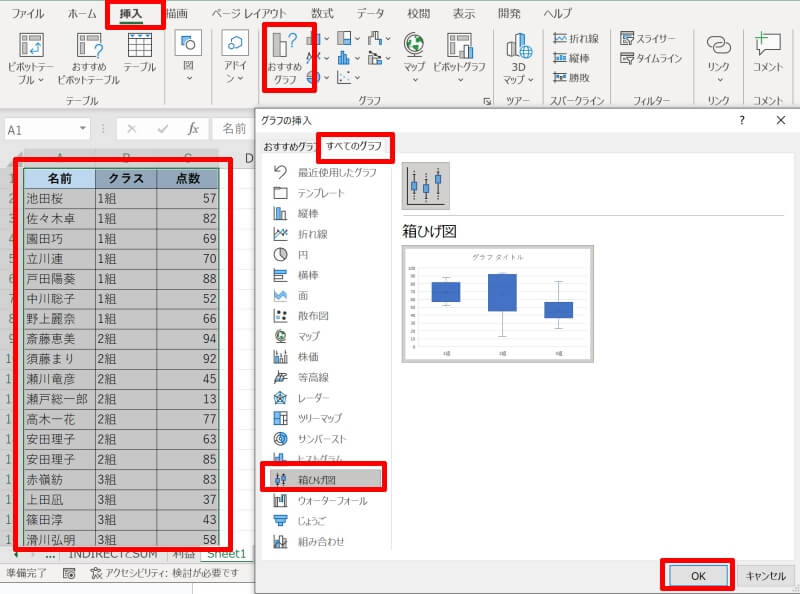
Excelの箱ひげ図(グラフ)の見方
Excel(エクセル)の箱ひげ図(グラフ)は独自のルールに沿って作成されますので、見方を事前に学んでおく必要があります。
まずは箱ひげ図を読みとる上で欠かせない要素を詳しく解説していきます。
- 箱ひげ図の要素と見方
- 四分位数はデータを小さい方から均等に4分割した値
- 四分位範囲はデータの中央部分50%の範囲
- 外れ値は他の値から極端に離れた値
箱ひげ図の要素と見方
箱ひげ図は主に7つの構成要素から成り立っている図形です。これらの要素について、統計的な意味を理解していれば大まかなデータ分布をイメージできるようになるでしょう。

| 要素 | 意味 |
|---|---|
| 最大値 | 箱ひげ図によく用いられるルールとして、第3四分位数から四分位範囲×1.5離れた値とすることが多い。 |
| 最小値 | 箱ひげ図によく用いられるルールとして、第1四分位数から四分位範囲×1.5離れた値とすることが多い。 |
| 平均値(「×」のマーク) | 箱ひげ図では、データの平均値を×マークとして描画することがある。平均値も表すことで、より情報量の多いグラフとなる。 |
| 第一四分位数 | 四分位数の一つで、25パーセンタイルと同義。データを小さい順に並べたとき、初めから数えて25%の位置にある数。 |
| 第二四分位数(中央値) | 四分位数の一つで、50パーセンタイルや中央値と同義。データを小さい方から順に並べたとき、初めから数えて50%の位置にある数。 |
| 第三四分位数 | 四分位数の一つで、75パーセンタイルと同義。データを小さい順に並べたとき、初めから数えて75%の位置にある数。 |
| 外れ値 | 箱ひげ図によく用いられるルールとして、第1四分位数または第3四分位数から四分位範囲×1.5以上離れた値とすることが多い。明らかに他の数とかけ離れている値を外れ値とみなし、データセットから取り除くことができる。 |
四分位数はデータを小さい方から均等に4分割した値
四分位数とは第一四分位数、第二四分位数、第三四分位数をまとめた呼び名です。
データを小さい順に並べて、下から25%のところのデータを第一四分位数、50%のところのデータを第二四分位数(中央値)、75%のところのデータを第三四分位数と言います。
四分位数の求め方は、データの数が奇数個か偶数個かで計算方法が異なります。例えばデータが奇数個の場合は、小さい方から数えてちょうど真ん中にあるデータが第二四分位数(中央値)となります。
次に中央値を除いて小さいデータと大きいデータに分けます。それぞれのグループのデータ数は奇数個であるので、同様にそれぞれのグループの真ん中のデータを求めます。これがそれぞれ第一四分位数、第三四分位数となります。
一方、データが偶数個の場合、真ん中にくるデータ2つの平均値が第二四分位数(中央値)となります。今度は中央値を除かずに、そのままデータを真ん中で分割して小さいデータと大きいデータに分けます。データが偶数個の場合は同様に真ん中にくるデータ2つの平均値、データが奇数個の場合はちょうど真ん中にくるデータが第一四分位数、第三四分位数となります。
四分位範囲はデータの中央部分50%の範囲
四分位範囲はデータの第1四分位数から第3四分位数までの範囲(データの中央50%部分の範囲)のことを指し、ばらつきの大きさを知ることができます。四分位範囲が大きいほどデータのばらつきが大きくなり、小さいほどデータが集中していると言えます。
四分位範囲は第三四分位数から第一四分位数を引くことで求めることができます。先ほど説明した四分位数の求め方で求めた第一四分位数と第三四分位数の値を使用しましょう。
これで異なるグループのデータのばらつきの大きさを比較することができます。それぞれのグループの第一四分位数と第三四分位数を求め、四分位範囲を計算しましょう。四分位範囲が大きいグループのデータはばらつきが大きく、小さいグループのデータはばらつきが小さいということになります。
外れ値は他の値から極端に離れた値
外れ値は得られた観測値の中で他の値と比べて極端に離れた値のことです。外れ値のうち、測定の不備や記録ミスなどの原因が分かっているものを「異常値」と呼ぶこともあります。
外れ値や異常値などのデータのばらつきを用いて、例えば工場の製造工程に異常が発生していないかどうかを推測することができます。
データ分析をする際に、外れ値を異常として除外する場合があります。しかし外れ値が生じる原因は様々あるため、ミスや不備があった場合など確実に理由が分かる時を除いて即座に値を除外しないようにしましょう。
外れ値が生じた原因を追及することで、新たな発見が隠されている場合があります。値を除外するかどうかは慎重に検討することが重要です。
Excelの箱ひげ図の作り方
それではExcel(エクセル)を用いて実際に箱ひげ図を作成してみましょう。ここでは例として、1~3組の試験の成績の分布を比較したいと思います。
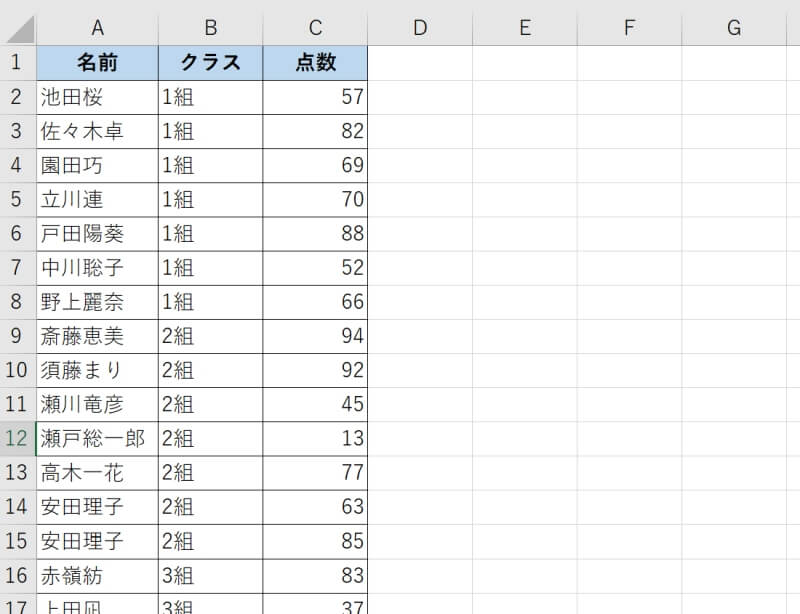
例のようなデータを用意しましょう。必要な要素としては、比較したいグループの項目とそれぞれのグループに属するデータです。例ではグループの名称として1組、2組、3組を、それぞれのクラスの生徒の成績をデータとしてまとめた表を作成しています。
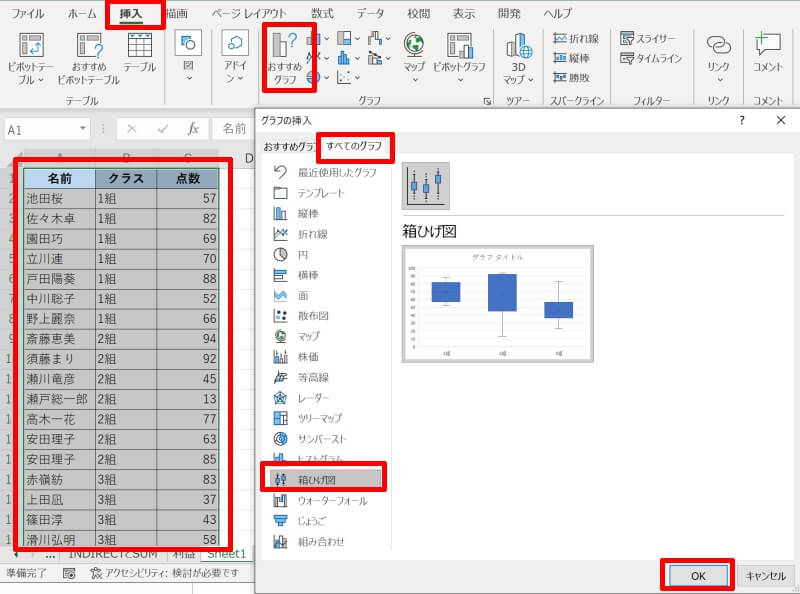
グラフを作成したいデータを全て選択し、グラフを作成するための手順を実行します。まず「挿入」タブの「グラフ」にある「おすすめグラフ」を選択しましょう。
「グラフの種類の変更」という画面が表示されるので、「すべてのグラフ」タブから「箱ひげ図」を選んでOKを押しましょう。
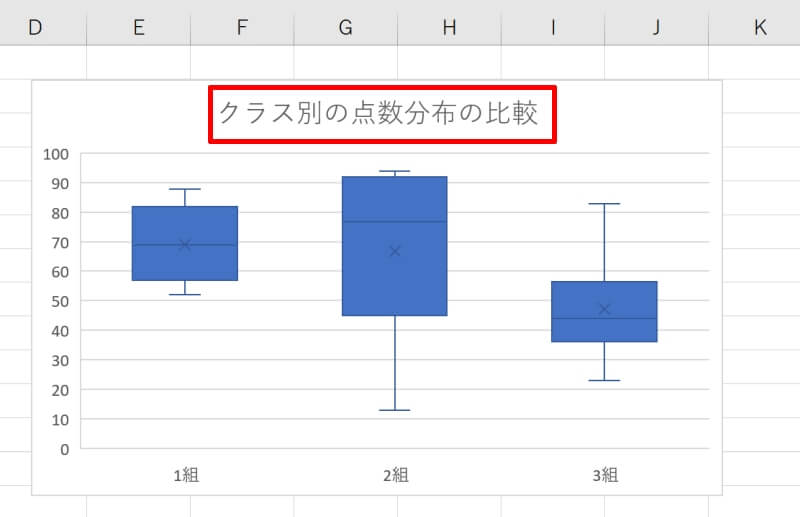
グラフのタイトルを変更しましょう。なるべく端的にグラフの内容を説明したタイトルをつけます。
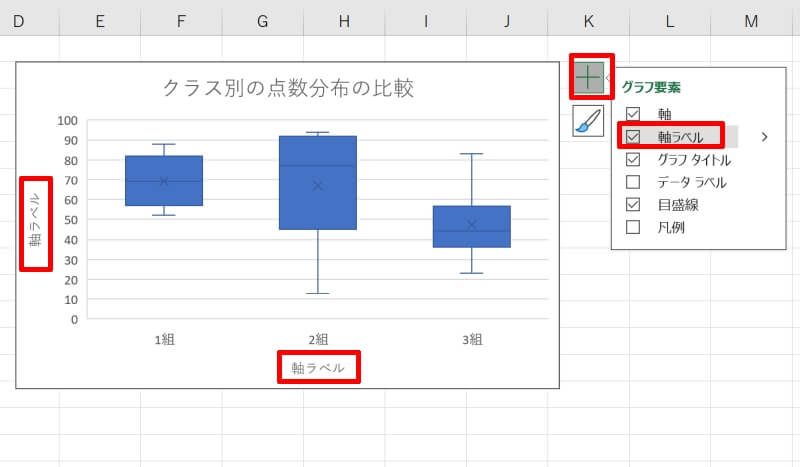
縦軸や横軸の項目が不明瞭な時は軸ラベルを設定しましょう。グラフを選択して、グラフの右側に出てくる「+」のアイコンを左クリックしましょう。グラフ要素の設定画面から「軸ラベル」にチェックを入れてください。
軸ラベルが追加されるので適切な名称を入力します。例では、縦軸が「試験の点数」で横軸が「クラス」となります。
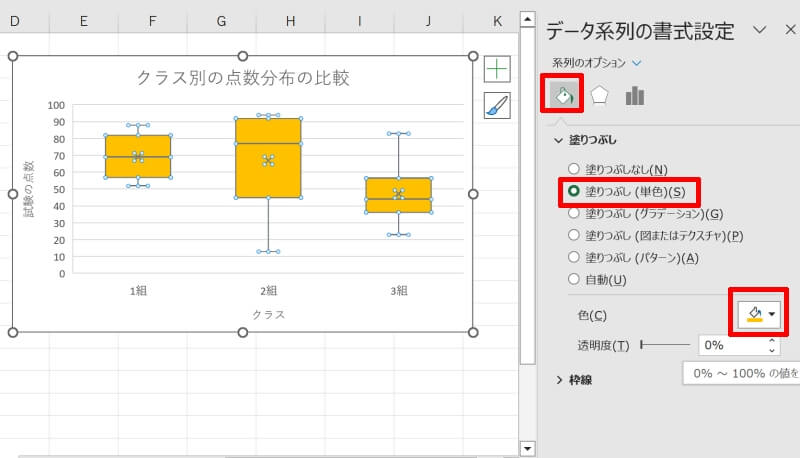
デフォルトではグラフは濃い青色に設定されていますが、四分位数や平均を表す×印が見づらいのであれば、グラフの色を変更しましょう。グラフ上でダブルクリックすると、右側にデータ系列の書式設定画面が出てきます。「塗りつぶしと線」のタブから「塗りつぶし」の色を変更しましょう。
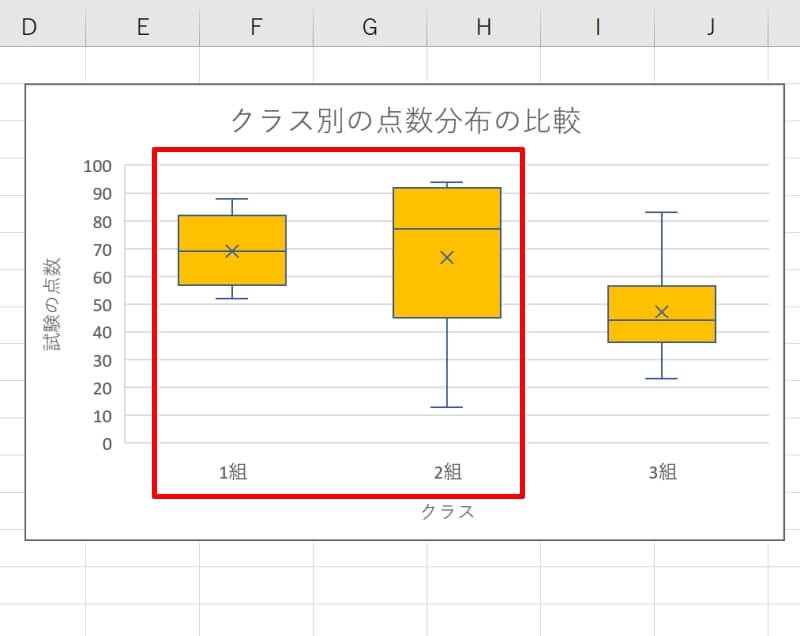
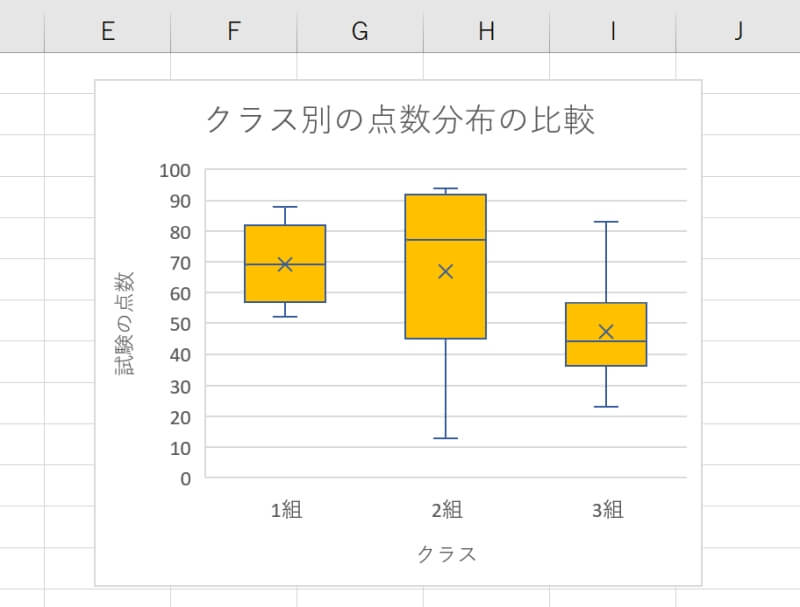
作成したグラフを元に、各グループのデータ分布やばらつきの大きさを比較します。例では、1組と2組の平均点は70点くらいで同じですがばらつきの程度が大きく異なります。1組は比較的平均点付近にデータが集まっておりばらつきは小さいと言えますが、2組は四分位範囲が広くばらつきが大きいと言えます。
このように平均点を見ただけでは、多数の学生が理解できていると考えられるのか、実は理解できた学生とできていない学生が2極化していると考えられるのか分かりません。
多くの情報をまとめて可視化できる箱ひげ図を有効に活用できるようになると、よりデータの持つ意味を明らかにすることができるでしょう。ぜひ従来業務の改善や新知見の探索などにつなげてみてください。
Excelの箱ひげ図で平均線・平均マーカーを表示・非表示にする方法
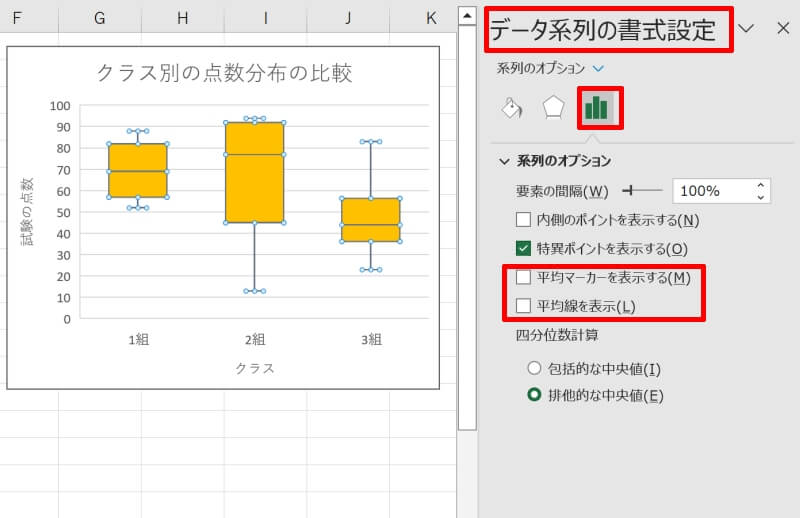
Excel(エクセル)で作成した箱ひげ図の平均線・平均マーカーを表示・非表示にする方法を紹介します。
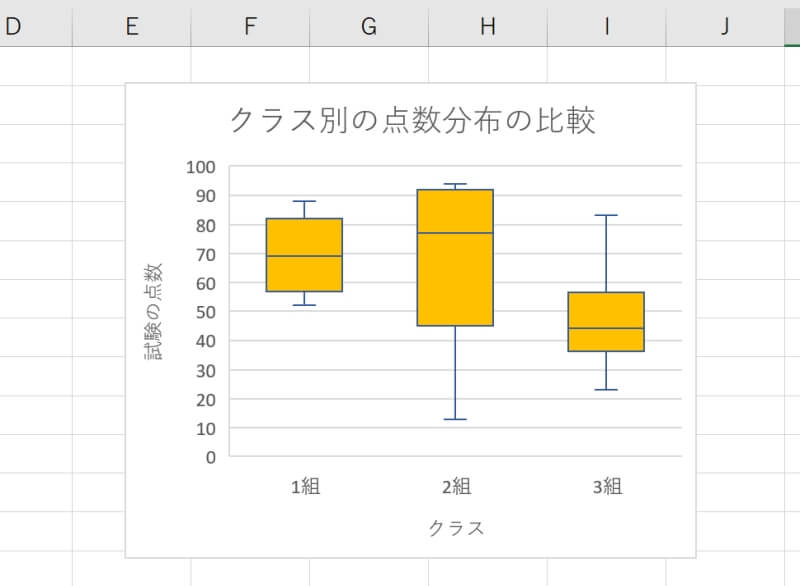
平均線・平均マーカーを表示したい場合はチェックを入れ、非表示にしたい場合はチェックを外します。
Excelの箱ひげ図で外れ値の表示・非表示を切り替える方法
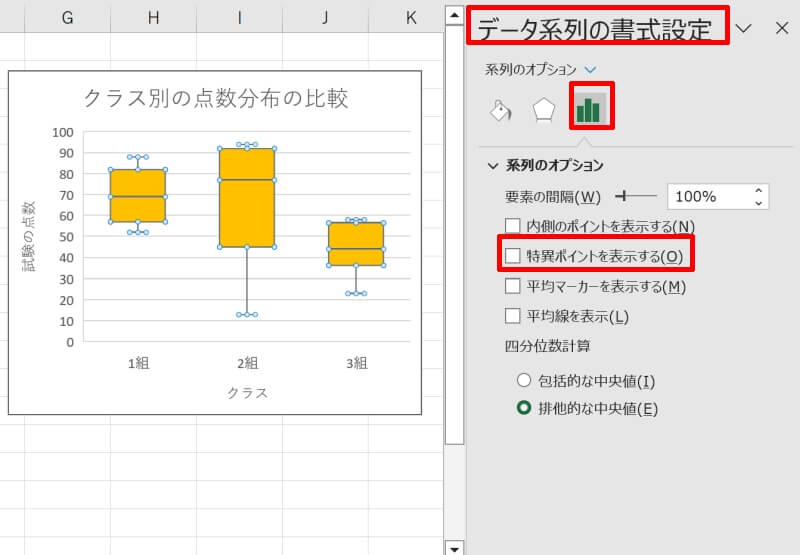
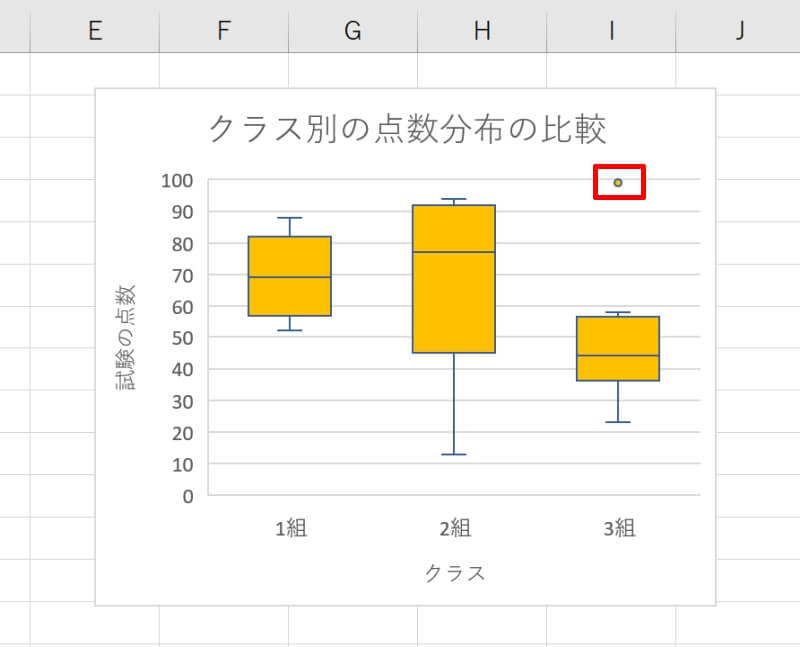
Excel(エクセル)で作成した箱ひげ図の外れ値の表示・非表示を切り替える方法を紹介します。
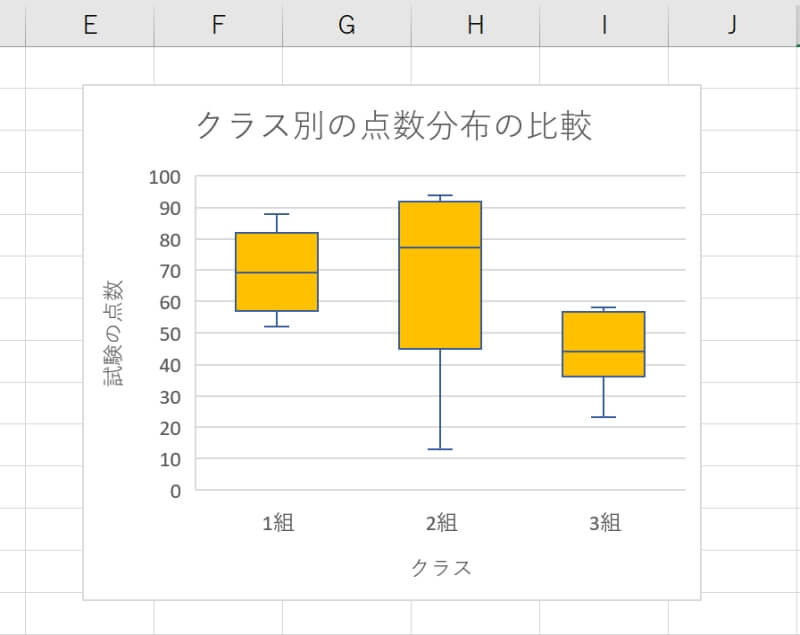
外れ値を表示したい場合はチェックを入れ、非表示にしたい場合はチェックを外します。
Excelの箱ひげ図についておさらい
Excel(エクセル)の箱ひげ図について、グラフの読み取り方から作成方法まで解説しました。直感的でない分訓練が必要かもしれませんが、使いこなせるようになるとワンランク上のデータ分析が可能になるでしょう。
単に箱ひげ図の作成ができるだけでなく、実務に活かして意味のある統計解析ができるようにくり返し練習してみましょう。
リテラアップアプリのご利用について、法人の方は下記フォームよりお問い合わせください。
(Excel,WordなどOffice製品やPC関連の技術的な質問にはお答えできかねます。ご了承ご了承ください。)





