エクセル関数で分散を求める方法｜標本分散と不偏分散

エクセル関数で分散を求める方法を紹介します。近年データサイエンスなどの分野を扱う機会が増えています。大量のデータや情報を取得できるようになり、そのデータをうまく統計手法を使って分析することが求められているのでしょう。

ここでは、統計でよく扱われる統計量である標本分散や不偏分散とは何か？といった内容や、エクセルでそれらの統計量を求めるための方法を解説していきます。

分散とは

分散とは、統計学において数値データのばらつき度合い（散らばり度合い）を表すための指標のことです。平均値から外れた値をとるデータが多いほど分散が大きく、ばらつきの大きいデータ群と考えることができます。

例えばテストの点数を横軸、その点をとった人数を横軸にした度数分布を2つ見てみましょう。左は平均点に近い点数をとった生徒が多く、右は平均点から離れた点数をとった生徒が多いと言えます。

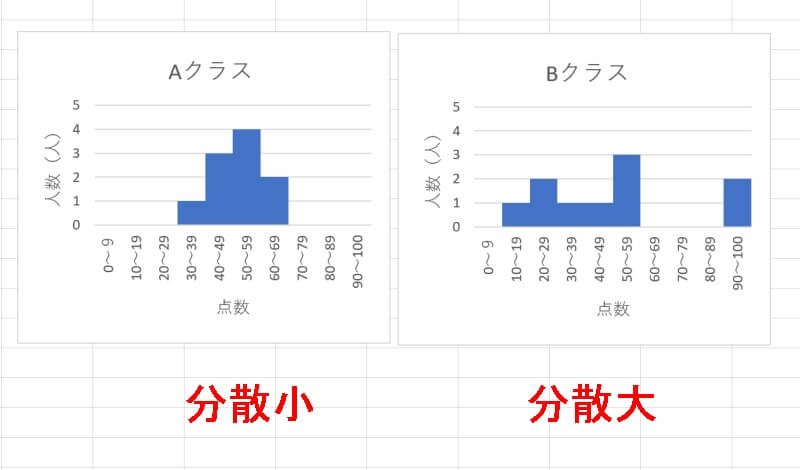
この時、左のデータ群は分散が小さく、右のデータ群は分散が大きいということになります。

分散の計算の仕方は、平均値と個々のデータの差の2乗の平均を求めることによって計算され、画像のような計算式になります。

例えばテストの例ですと、各データは「各生徒の点数」、平均は「テストの平均点」、データの総数は「生徒の人数」となります。

エクセルで標本分散を求める方法【VAR.P関数】

エクセルでVAR.P（バリアンス・ピー）関数を用いて標本分散を求める方法を紹介します。

標本分散の基礎知識やVAR.P関数の書式、具体的な使い方を丁寧に解説していますので、統計を初めて学ぶ方も参考にしてみてください。

標本分散とは

標本分散は標本から計算した分散のことで、標本のばらつきを表す指標となります。統計対象となる全ての集合である母集団に対して、標本とは母集団から抽出した部分集合（一部のデータ群）となります。

母集団の平均・分散・標準偏差のことを母平均・母分散・母標準偏差と言い、これは真の値です。しかし現実的には母集団全てのデータを分析することは難しいので、標本となるデータ一部を抜き出し、標本平均・標本分散・標本標準偏差として取り扱うのです。

標本分散を求めるVAR.P関数の書式

標本分散を求める時に使用する、VAR.P（バリアンス・ピー）関数の書式を紹介します。

VAR.P（数値1, 数値2, …, 数値255）

VAR.P関数の引数は255まで指定することができますが、必須な引数は1つのみです。標本分散を求めたい数値を直接引数として入力する以外に、該当するセル範囲を指定してもOKです。

標本分散をVAR.P関数で求める方法

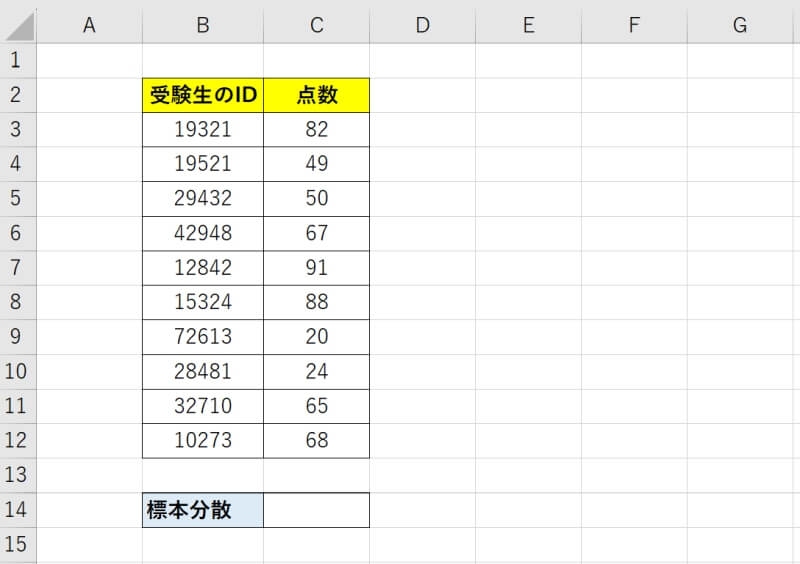
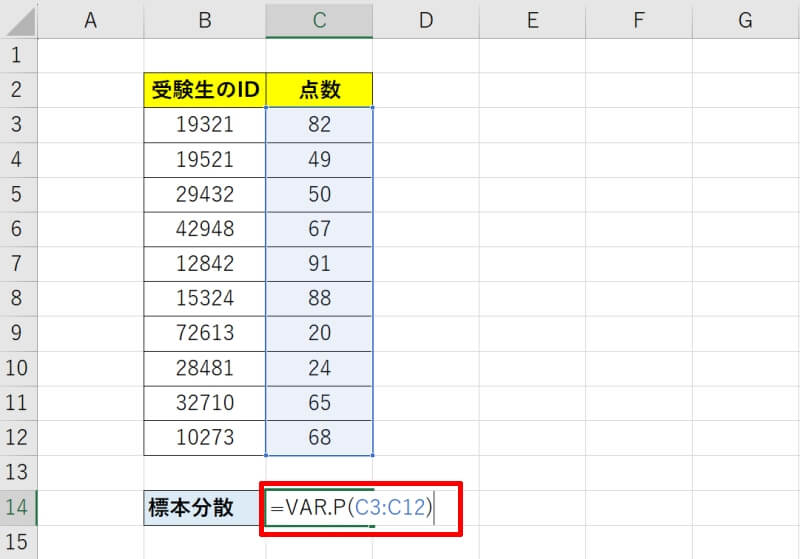
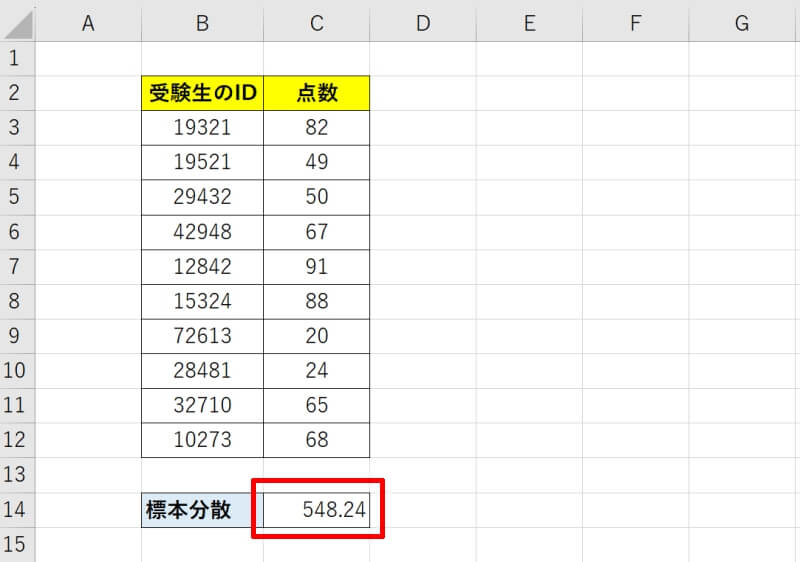
VAR.P関数を使用して標本分散を求める方法を具体的例を交えて説明します。

エクセルで不偏分散を求める方法【VAR.S関数】

次は、エクセルで不偏分散を求める方法を紹介します。今度はVAR.S（バリアンス・エス）関数を使用します。標本分散の時と同様に、不偏分散の基礎知識からVAR.S関数の書式、具体的な使い方まで詳しく見ていきましょう。

不偏分散とは

不偏分散とは、標本の偏りを除いて母集団の分散を推定するために使われるものです。

先ほど述べたように、母集団を調査することは現実的に難しいことが多いため標本から母集団を推定します。標本分散の期待値は母分散の (n-1)/n 倍になることが分かっていますので、母分散を推定する不偏分散の式は以下のようになります。

不偏分散＝(n-1)/n×標本分散

分散と一口に言っても標本分散と不偏分散の2種類がありますが、省略されて分散とのみ書かれることがあります。このような場合は文脈で判断する必要がありますので注意しましょう。

不偏分散を求めるVAR.S関数の書式

不偏分散を求めるVAR.S（バリアンス・エス）関数の書式を紹介します。

VAR.S（数値1, 数値2, …, 数値255）

VAR.P関数と同様、引数は255まで指定することができますが必須な引数は1つのみです。不偏分散を求めたい数値を直接引数として入力する以外に、該当するセル範囲を指定してもOKです。

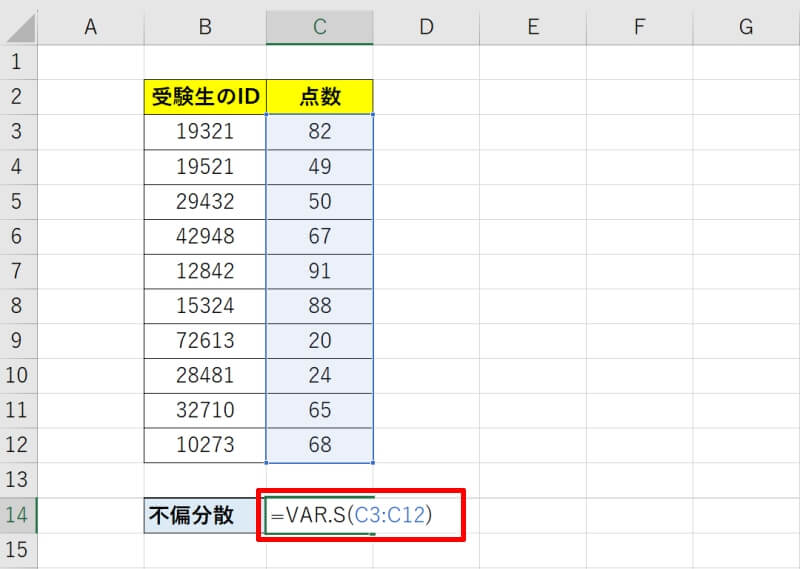
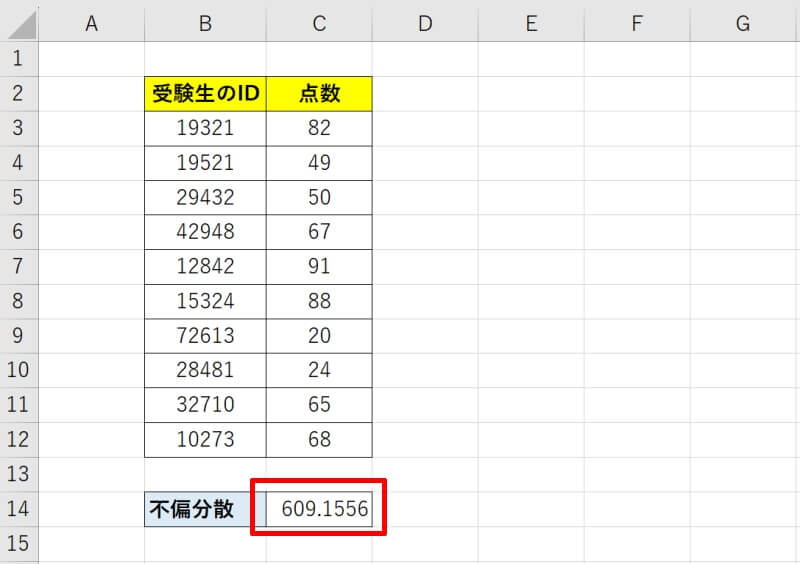
不偏分散をVAR.S関数で求める方法

不偏分散をVAR.S関数で求める方法を具体的に見ていきましょう。先ほど使用した、ある試験をA会場で受けた人の結果を用いて不偏分散を求めていきます。

エクセル関数で標準偏差を求める方法【STDEV.P関数】

最後にエクセル関数のSTDEV.P（スタンダード・ディビエーション・ピー）関数を使って標準偏差を求める方法を解説します。

先ほど紹介した2つは「分散」でしたが、今度は「偏差」を求めることになります。似ている概念ですので間違えないようにしましょう。

標準偏差とは

標準偏差とは、データが平均値の周辺でどれくらいばらついているかを表す指標です。分散と同じくばらつきを表すものですが、標準偏差は分散の平方根を取ったものになります。

これは、分散の単位の次元が使用したデータの単位の次元と異なるためです。感覚的に使用したデータと単位が同じ方が理解しやすいので、このような処理を行ないます。

試験でよく用いられる偏差値は、自分の得点から平均値を引いた値を標準偏差で割って 10倍し、それに50を加えたものです。

標準偏差を求めるSTDEV.P関数の書式

標準偏差を求めるSTDEV.P（スタンダード・ディビエーション・ピー）関数の書式です。

STDEV.P（数値1, 数値2, …, 数値255）

VAR.P関数やVAR.S関数と同様、引数は255まで指定することができますが必須な引数は1つのみです。標準偏差を求めたい数値を直接引数として入力する以外に、該当するセル範囲を指定してもOKです。

標準偏差をSTDEV.P関数で求める方法

標準偏差をSTDEV.P関数で求める方法を具体的に見ていきましょう。ここでも、ある試験をA会場で受けた人の結果を用いて標準偏差を求めていきます。

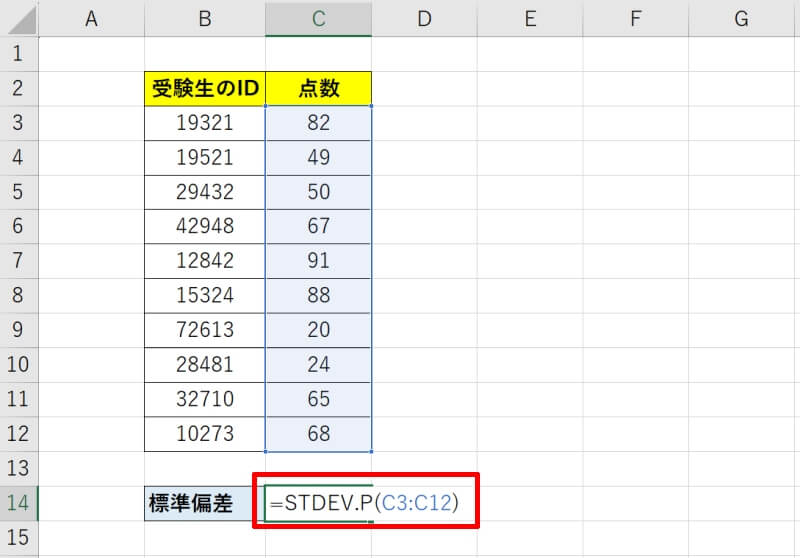
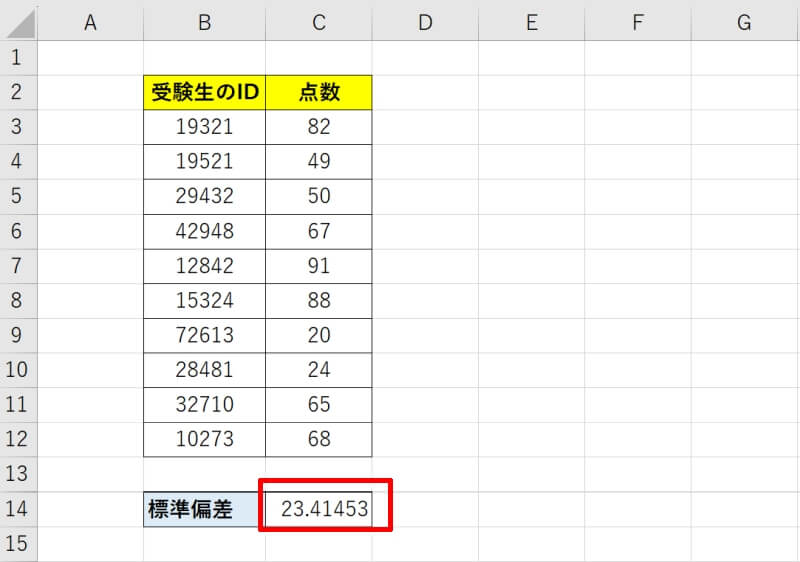
標本の標準偏差は標本分散の平方根を取ったものと一致します。今回の例でも標本分散は548.2、標準偏差は23.41（=√548.2）となり、一致します。

エクセル関数で分散を求める方法をおさらい

エクセル関数で分散や偏差を求めるための関数を3種類紹介しました。

• 標準分散はVAR.P関数
• 不偏分散はVAR.S関数
• 標準偏差はSTDEV.P関数

単に関数の使い方を覚えるだけではなく、それぞれの統計的な意味も抑えておくことが肝心です。説明を読むだけでは理解しづらい点もあると思いますので、例題や実例をたくさん学ぶことをおススメします。